######### Get the data#################
data("iris")
str(iris)
Output:
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
############training datasets and test datasets building #################
set.seed(111)
ind <- sample(2, nrow(iris),
replace = TRUE,
prob = c(0.8, 0.2))
training <- iris[ind==1,]
testing <- iris[ind==2,]
#########Scatter Plot & Correlations#check the correlation between variables########
install.packages("psych")
library(psych)
pairs.panels(training[,-5],
gap = 1,
bg = c("orange", "pink", "yellow")[training$Species],
pch=22)Output:
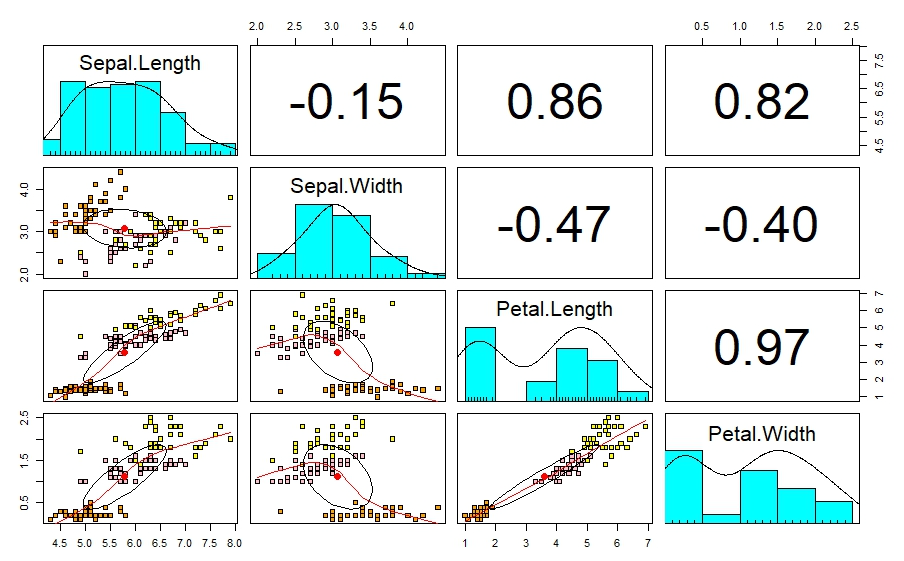
According to this petal length and petal width, sepal length and petal length , Sepal length, and petal width are highly correlated. This leads to multicollinearity. This issue can be reduce using PCA analysis.
#############Principal Component Analysis########################
pca <- prcomp(training[,-5],
center = TRUE,
scale. = TRUE)
attributes(pca)
[1] "sdev" "rotation" "center"
[4] "scale" "x"
$class
[1] "prcomp"
pca$center
Sepal.Length Sepal.Width Petal.Length
5.8 3.1 3.6
Petal.Width
1.1
pca$scale
Sepal.Length Sepal.Width Petal.Length
0.82 0.46 1.79
Petal.Width
0.76
print(pca)
Output:
Standard deviations (1, .., p=4):
[1] 1.7173318 0.9403519 0.3843232 0.1371332
Rotation (n x k) = (4 x 4):
PC1 PC2 PC3 PC4
Sepal.Length 0.5147163 -0.39817685 0.7242679 0.2279438
Sepal.Width -0.2926048 -0.91328503 -0.2557463 -0.1220110
Petal.Length 0.5772530 -0.02932037 -0.1755427 -0.7969342
Petal.Width 0.5623421 -0.08065952 -0.6158040 0.5459403
###########summarized#####################
summary(pca)
Output:
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7173 0.9404 0.38432 0.1371
Proportion of Variance 0.7373 0.2211 0.03693 0.0047
Cumulative Proportion 0.7373 0.9584 0.99530 1.0000
######scatter plot## To check the correlation between the principal components ####
pairs.panels(pca$x,
gap=0,
bg = c("orange", "pink", "yellow")[training$Species],
pch=22)
Output:
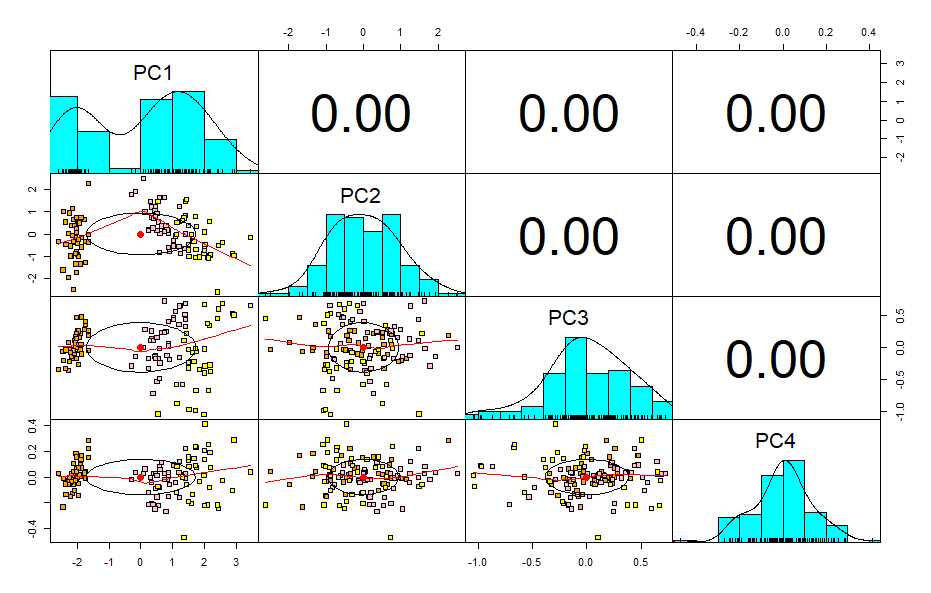
Now there is no correlation between multiple variables therefore there is no multicollinearity issue.
######### explain the PCA using BY BIPLOT################
library(devtools)
install_github("vqv/ggbiplot")
library(ggbiplot)
g <- ggbiplot(pca,
obs.scale = 1,
var.scale = 1,
groups = training$Species,
ellipse = TRUE,
circle = TRUE,
ellipse.prob = 0.68)
g <- g + scale_color_discrete(name = '')
g <- g + theme(legend.direction = 'horizontal',
legend.position = 'top')
print(g)
Output:

BIPLOT is useful to understand what is happening in the data set.
- PC1 is positively correlated with the variables Petal Length, Petal Width, Sepal Length,negatively correlated with Sepal Width.
- PC2 is negatively correlated with Sepal Width.
References
- Principal component analysis (PCA) in R | R-bloggers. (2021, May 7). Principal Component Analysis (PCA) in R | R-bloggers. https://www.r-bloggers.com/2021/05/principal-component-analysis-pca-in-r/
